UNIVERSO OLOFRATTALE
“La
filosofia naturale è scritta in questo grandissimo libro che continuamente ci
sta aperto innanzi agli occhi, io dico l’universo, ma non si può intendere se
prima non s’impara a intender la lingua e conoscer i caratteri nei quali è
scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli,
cerchi ed altre figure geometriche, senza i quali mezzi è impossibile a
intenderne umanamente parola; senza questi è un aggirarsi vanamente per un
oscuro labirinto.” Il Saggiatore, Galileo Galilei (1564-1642)
Quando Due anni fa iniziai lo studio della “Geometria Sacra” intuivo l’estrema importanza di questa materia ma non riuscivo a comprendere il legame fra i vari concetti matematici e geometrici che contenuti in essa, sembrava non esistesse un filo conduttore fra i vari argomenti.
La
geometria dei frattali è riuscita a dare coerenza a questo mio intero percorso
di studio, i Frattali sono la summa dei principi della geometria sacra,
contengono nella loro meccanica il set principale di leggi naturali che
regolano la creazione di un microcosmo come di un macrocosmo, essi sono il modo
in cui l’Intelligenza Universale, il Logos, manifesta la sua Creazione nella
Realtà che percepiamo.
Per
il loro sviluppo i frattali seguono le leggi note come la Sequenza
di Fibonacci,
La spirale
Logaritmica, il
Rapporto
Aureo Phi
1,618, Il
Phi Greco π, le Radici Quadrate di due tre e cinque, i concetti di Zero ed Infinito, la
geometria dei Solidi Platonici e la Multi-dimensionalità in scale
differenti.
I
Frattali implicano l’auto-similarità, strutture di questo tipo possono essere
ripetute più volte creando forme apparentemente diverse fra loro ma simili nel
loro intimo, i frattali sono un modello valido comunque ed ovunque. I frattali
sono la geometria più efficiente per poter contenere un numero teoricamente
infinito di spazio lineare in un’area finita, è così che la natura riesce a
fare contenere 96000
metri di vene e arterie in un corpo umano.
La
teoria dei frattali riesce a trovare l’Ordine implicito nell’apparente
Caos dei modelli naturali, essa riesce a spiegare come una foglia contenga
nella sua struttura l’immagine dell’albero a cui appartiene o l’esatta
direzione con cui un fulmine si propagherà nell’atmosfera.
Video su Scarabeokheper.altervista.org
Un
buon modo per cominciare a comprendere i concetti che intendo esporre in questo
testo consiste nel visionare questa magnifica video-intervista a Benoit
Mandelbrot Video: I
Frattali e la Matematica di Benoit Mandelbrot, dove Mandelbrot in persona
racconta la la sua esperienza di ricercatore dedicata allo studio della
matematica e della geometria culminata con la scoperta della Geometria Dei
Frattali e le applicazioni di tale teoria in molti campi della ricerca,
dall’elettronica alla medicina.
BIOGRAFIA MANDELBROT
Benoît
Mandelbrot (Varsavia, 20 novembre 1924–Cambridge, 14 ottobre 2010) è stato un
matematico polacco naturalizzato francese, noto per i suoi lavori sulla
geometria frattale. Nato in Polonia da una famiglia ebrea di origini lituane,
ha vissuto in Francia per buona parte della sua vita. È nato in una famiglia
con forte tradizione accademica: sua madre era laureata in medicina, e suo zio
Szolem Mandelbrot era un famoso matematico specialista in analisi matematica;
suo padre si occupava della vendita di abiti.
Nel 1936 la famiglia lasciò la Polonia, stabilendosi a Parigi. A Parigi fu iniziato alla matematica dai suoi due zii, che contribuirono alla sua educazione e formazione, sia scientifica che umanistica. Nel 1939, a causa dello scoppio della guerra, si trasferì con la famiglia a Tulle, un paesino della Francia centrale, dove si diplomò nel 1942.
Educato
in Francia, ha sviluppato la matematica di Gaston Julia e ha dato inizio alla
rappresentazione grafica di equazioni su computer. Mandelbrot è il fondatore di
ciò che oggi viene chiamata geometria frattale, e ha dato il proprio nome a una
famiglia di frattali (detti appunto frattali di Mandelbrot) e a un particolare
insieme (detto insieme di Mandelbrot).
A
partire dai primi anni sessanta, e fino ai giorni nostri, l’applicazione della
geometria frattale a questioni economiche ha condotto Mandelbrot a mettere in
discussione alcuni consolidati fondamenti dell’economia classica e della
finanza moderna, quali l’ipotesi di razionalità dei comportamenti degli agenti
economici, l’ipotesi dell’efficienza del mercato, e quella secondo cui i
movimenti dei prezzi di mercato sono descrivibili come un cammino casuale
(random Walk) in analogia al moto browniano di una particella in un fluido.
Mandelbrot
scoprì il suo frattale quasi per caso nel 1979, mentre conduceva degli
esperimenti per conto del Thomas J. Watson Research Center dell’IBM, dove, con
l’aiuto
della
computer grafica, poté in seguito dimostrare che il lavoro di Julia del 1918 (e
che suo zio gli aveva consigliato nel 1945), poteva essere uno dei frattali più
affascinanti; una delle numerose curiosità del frattale di Mandelbrot è che esso
comprende, pur nella sua semplicissima formula, anche il frattale di
Julia.
I suoi lavori sui frattali in quanto matematico impiegato all’IBM gli hanno fruttato una “Emeritus Fellowship” ai laboratori di ricerca T. J. Watson.
L’analisi
frattale delle variabili economiche e finanziarie ha portato nell’ultima decade
alla nascita della cosiddetta finanza frattale, nella quale lo stesso
Mandelbrot ritiene siano attualmente impegnati almeno un centinaio di
ricercatori. Altri ricercatori sono impegnati nel più vasto campo
dell’econofisica.
Oltre
alla riscoperta dei frattali in matematica, dimostrò che essi possono essere la
chiave di lettura delle forme presenti in natura, dando il via a una
particolare sezione della matematica che studia la teoria del caos. Nel 1993
gli è stato conferito il prestigioso Premio Wolf per la Fisica, “per aver
trasformato la nostra visione della natura”. Il 19 marzo 2007 ha tenuto una “Lectio
Magistralis” dal titolo “Il liscio, il ruvido e il meraviglioso” durante il
Festival della Matematica a Roma.
Numerose
università del mondo gli hanno conferito la laurea honoris causa; in Italia
l’Università degli studi di Bari gliene ha conferita una in Medicina e
Chirurgia il 13 novembre 2007 con la seguente motivazione: “La visione
altamente unificante del fenomeno della vita che ci offre il professor
Mandelbrot, si riflette in campo medico con un approccio unitario, prima
sconosciuto, alla malattia e alla persona malata”. In occasione del
conferimento della laurea, il prof. Mandelbrot ha tenuto una lectio magistralis
intitolata “Fractals in Anatomy and Physiology”, nella quale fra l’altro
affermava:« Il concetto di base che unisce lo studio dei frattali alle
discipline come la biologia e quindi anatomia e fisiologia parte dalla
convinzione di un necessario superamento della geometria euclidea nella
descrizione della realtà naturale. Volendo essere molto sintetici, i frattali
servono a trovare una nuova rappresentazione che parta dall’idea di base che
il piccolo in natura non è nient’altro che una copia del grande. La mia
convinzione è che i frattali saranno presto impiegati nella comprensione dei
processi neurali, la mente umana sarà la loro nuova frontiera. » Mandelbrot
muore il 14 ottobre 2010, all’età di 85 anni, a causa di un cancro del pancreas
I FRATTALI
Per
poter comprendere i concetti di “Frattale” e di “Attrattore” è necessario che
prima di continuare nella lettura guardiate con attenzione questo video, dove
Mandelbrot e Lorenz parlano in prima persona delle loro scoperte: Frattali documentario –
YouTube.
DEFINIZIONE DI FRATTALE
“La
geometria euclidea è incapace di descrivere la natura nella sua complessità, in
quanto si limita a descrivere tutto ciò che è regolare. Tutti gli oggetti che
hanno una forma perfettamente sferica, oppure… mentre osservando la natura
vediamo che le montagne non sono dei coni, le nuvole non sono delle sfere, le
coste non sono dei cerchi, ma sono oggetti geometricamente molto complessi.”
(da Les objects fractals 1975”)
I frattali sono delle speciali figure geometriche che presentano in maniera ripetitiva e dettagliata, ad ogni livello di ingrandimento, una struttura auto-similare (per cui ogni porzione del frattale è una riproduzione – analoga, non identica – su scala ridotta dell’intera figura). Il termine frattale è stato coniato nel 1975 dal matematico Benoit Mandelbrot (derivandolo dal latino “fractus” – frazionario) ma in effetti già dalla fine dell’800 i matematici avevano incontrato alcune figure dalle proprietà anomale che avevano definito “mostri matematici”, una tra le più famose è la Curva di Koch che trasformando ognuno dei suoi 3 segmenti iniziali in 4 sotto-segmenti e ripetendo indefinitamente il processo, da origine ad una figura che pur essendo delimitata in uno spazio finito possiede una lunghezza infinita.
Una
delle “strane” peculiarità di un frattale è che non può mai essere disegnato
completamente, e infatti ciò che vediamo di esso è solo un’iterazione
finita (l’iterazione è la ripetizione del calcolo della formula che
definisce il frattale), mentre per loro stessa concezione i frattali sono
strutture complesse e non finite, ad ogni ingrandimento rivelano dettagli
precisi, sempre nuovi, che solo il calcolo mediante il computer ha permesso di
rappresentare graficamente. Nei frattali esiste dunque la possibilità di
iterare virtualmente all’infinito ciascun punto della figura prima di passare
al successivo, ed è proprio per questo che la dimensione occupata nello spazio
dai frattali non è una dimensione finita (come nel caso delle figure
elementari della geometria: D1=linea, D2=quadrato, D3=cubo), bensì una dimensione
frazionaria, concetto questo che mette a dura prova la capacità di
immaginazione.
In
generale un frattale è un insieme che gode di una o più proprietà seguenti:
Auto-somiglianza: è l’unione di copie di se stesso a scale differenti;
Struttura fine: il dettaglio dell’immagine non cambia ad ogni ingrandimento;
Irregolarità:
non si può descrivere come luogo di punti che soddisfano semplici condizioni
geometriche o analitiche; la funzione è ricorsiva ed irregolare localmente e
globalmente;
Dimensione Frattale: sebbene possa essere rappresentato in uno spazio
convenzionale a due o tre dimensioni, la sua dimensione non è
necessariamente un intero; può essere una frazione, ma spesso anche
un numero irrazionale. E di solito maggiore della dimensione topologica.
La
dimensione frattale è quindi il numero che misura il grado di irregolarità e di
interruzione di un oggetto, considerato in qualsiasi scala.
Da
quando Mandelbrot ha introdotto la geometria frattale, è nato un nuovo
linguaggio di descrizione delle forme complesse della natura: essi richiedono
algoritmi, semplici funzioni ricorsive, che, iterate un gran numero di volte,
forniscono un’immagine.
AMBITO DI APPLICAZIONE DEI FRATTALI
Negli
anni ’80 con tale nuova geometria si sono trovati frattali in ogni ambito:
dalla natura, alla medicina, alla musica e si è sviluppata una branca della
geometria frattale che studia i cosiddetti frattali biomorfi (studia le forme
della natura come il corallo etc.); inoltre si parla anche di frattali con
condensing, che utilizzano le trasformazioni geometriche del piano, i metodi
IFS ed L-System. I frattali sono usati da fisici e ingegneri nello studio dei
sistemi dinamici, per costruire modelli che descrivono il moto dei fluidi
turbolenti ed i fenomeni di combustione; ma secondo gli autori sono importanti
anche per le dimensioni extra e per la descrizione della gravità. Inoltre i
frattali trovano applicazione nella compressione delle immagini trasmesse e dei
film virtuali, nella distribuzione degli errori su certe linee telefoniche,
nello studio dei terremoti, degli uragani, del DNA, del cuore, dei vasi
sanguigni, del moto ondoso degli oceani, la riproduzione di mezzi porosi, lo
studio degli idrocarburi e della Natura in generale: coste geografiche, corso
dei fiumi etc.
STORIA DEI FRATTALI
In
questo Testo trovate un’ottima analisi dei frattali classici come la Curva di
Koch , il triangolo di Sierpinski , la polvere frattale di Cantor , La curva di
Peano e la curva di Hilbert .
PDF:
frattali
e sezione aurea.
Un
attrattore è un insieme a cui tende un sistema dinamico in un intervallo di
tempo piuttosto lungo. Un insieme è considerato attrattore solo se le
traiettorie ottenibili del sistema dinamico rimangono sempre vicine ad esso;
può essere un punto, una curva o forme frattali più complicate e se la
dimensione non è intera viene definito attrattore strano . Il termine fu
coniato da David Ruelle e Floris Takens per descrivere le biforcazioni di un
sistema che descrive il flusso di un fluido. È usato spesso nei sistemi
dinamici caotici e dissipativi (non esistono sistemi conservativi: sono
ideali). I sistemi dissipativi sono caratterizzati dal fatto che le orbite, pur
partendo da condizioni iniziali anche completamente diverse, finiscono per
giungere tutte in un determinato insieme di stati, detto attrattore.
Consideriamo,
ad esempio, un pendolo che oscilli: il suo moto si smorza progressivamente, con
oscillazioni sempre più piccole, fino a esaurirsi nella quiete. L’orbita di
fase è una spirale che termina nel punto velocità nulla, spostamento nullo, che
è il punto di equilibrio del pendolo. Tutte le orbite finiscono in questo
punto: esso è dunque l attrattore del sistema. Non tutti gli attrattori sono
costituiti da semplici punti; possiamo avere delle curve regolari, dette cicli
limite , oppure, nel caso dei sistemi caotici, delle strutture ancor più
insolite detti attrattori strani.
Esempio
di Ciclo Limite.
Ma
in pratica le traiettorie di un sistema dinamico non devono soddisfare nessuna
particolare proprietà, tranne che stare sull’attrattore e le traiettorie
possono essere periodiche, caotiche o altro. Una traiettoria periodica di un
sistema può essere governata da più di una frequenza. Se due di queste
frequenze sono in rapporto irrazionale (cioè sono incommensurabili), la
traiettoria non sarà più chiusa, e il ciclo limite diventa un toro limite.
Questo
tipo di attrattore viene chiamato Nt-toro se sono presenti Nt frequenze
incommensurabili.
GLI STRANI ATTRATTORI DEL CAOS
Consideriamo
una particella confinata in una determinata zona dello spazio, la quale sia
soggetta a certe leggi deterministiche. Seguendone l’evoluzione, probabilmente
noteremo che essa tenderà ad assestarsi in corrispondenza di uno fra tre
comportamenti possibili la cui descrizione geometrica è chiamata attrattore:
_La
particella può essere attratta verso una posizione di riposo finale (come un
pendolo che si ferma poco a poco); in questo caso l’attrattore è un punto.
_La
particella può stabilizzarsi in un ciclo periodico (come i pianeti nelle loro
orbite attorno al sole). In questo caso l’attrattore è un’ellisse e il moto
successivo può essere previsto con notevole precisione.
_L’ultima
possibilità è che la particella continui a vagare, muovendosi in modo erratico,
pur rimanendo confinata in una certa regione dello spazio. Il moto di alcuni
asteroidi rappresenta molto bene questo fenomeno.
Quest’ultima
possibilità è quella che ha le caratteristiche più interessanti. Si osserva
infatti che modestissimi errori nella misura della posizione e della
velocità dell’asteroide portano ad errori enormi nelle previsioni del
suo cammino futuro. Questo è il segnale del Caos, e le regioni dello spazio
individuate da questo moto sono dette Attrattori Strani.
Quando
una particella subisce l’influenza dell’attrattore strano, qualunque sia il
punto di partenza nelle vicinanze dell’attrattore, la particella si muoverà,
mediamente, sempre allo stesso modo, indipendentemente dal punto di partenza.
Il moto è determinato da leggi precise, ma la particella si comporta a tutti
gli effetti come se si muovesse a caso. Gli attrattori strani sono molto spesso
dei frattali.
ATTRATTORE DI MANDELBROT
“L’insieme
di Mandelbrot è il più noto dei grafici frattali ricorda talmente le immagini
della natura che è stato definito “L’impronta digitale di Dio”
Il
frattale di mandelbrot rappresenta graficamente un attrattore strano o caotico
che si divide sostanzialmente in 3 parti. la parte in nero rappresenta la zona
di attrazione verso lo zero, quella in bianco verso infinito, divise da un
confine circolare.
L
idea originale di Mandelbrot è stata di usare la semplice formula ricorsiva:
Zn+1 = Zn^2 + Zc
Con
Zn+1, Zn e Zc valori complessi e con Zc che rimane costante nella applicazione
ricorsiva della formula.
Se
Zn è un numero complesso qualunque, elevandolo al quadrato e sommando Zc
si ottiene un nuovo numero complesso.
Se
al risultato Zn+1 ottenuto si riapplica lo stesso procedimento, ovvero si
assume il risultato come Zn e si riapplica la formula indefinitamente, si
ottengono ulteriori valori.
Nel
caso in cui Zc sia nullo, si possono verificare tre possibilità:
Punti
che distano 1 dall’origine (cioè, che stanno su una circonferenza di raggio
r=1) non sono mossi dalla trasformazione (perché tali punti di zn+1 sono uguali
a zn, se zn=1);
Punti
che distano meno di 1 dall’origine, che sono cioè interni alla circonferenza di
r=1, si muovono verso l origine (perché zn+1 < zn, se zn<1);
Punti
che distano più di 1 dall’origine, che sono cioè esterni alla circonferenza di
r=1, si muovono verso l infinito (perché zn+1>zn se zn>1).
Ci
sono, dunque, due zone di attrazione , verso lo zero e verso infinito, divise
da un confine circolare.
Nel
caso in cui Zc sia diverso da zero, il risultato dipende dal valore: Per certi
valori di Zc, continuando ad applicare la regola, i punti nel piano si
allontana sempre di più e si dice che il percorso è imprevedibile o illimitato;
l insieme dei punti che scappano è l insieme di fuga.
Per
altri valori di Zc, il punto non fugge via , ma crea forme intricate di
straordinaria bellezza, In tal caso si dice che dà luogo ad un percorso
prevedibile o limitato o insieme prigioniero di punti e genera i frattali di
Mandelbrot.
Tra
fuggire all’infinito e rimanere in trappola vi è una grande differenza; ma
quali sono i valori della Zc costante che producono un certo comportamento? Per
scoprirlo, immaginiamo, ad esempio, di dividere il piano in piccole celle e
scegliamo una costante complessa al centro di una cella. Se la regola eleva al
quadrato ed aggiungi una costante porta alla fuga, coloriamo di bianco la
cella; se il punto rimane intrappolato, la coloriamo di nero. Facciamo la
stessa cosa con tutte le celle, una alla volta. Otteniamo così una forma
estremamente complicata: un frattale, detto insieme di Mandelbrot .
L’insieme
prigioniero e l’insieme di fuga sono separati da una frontiera molto stretta,
frontiera che assume il nome di insieme di Julia , in onore appunto del
matematico Gaston Julia. Come si fa a sapere se un punto è di fuga oppure
prigioniero?
La
risposta è data da un teorema dimostrato dallo stesso Mandelbrot: Se un punto
si trova ad una distanza maggiore o uguale a due unità dall’origine, allora è
destinato all’infinito; se invece si trova ad una distanza minore a due unità
dall’origine, allora è un punto prigioniero.
A
questo punto appare chiaro che, per ciascun valore prefissato di Zc usato nella
formula di iterazione, appare un diverso insieme di Julia, pieno di
prigionieri. I punti prigionieri ovviamente costituiscono l’insieme di
Mandelbrot la cui forma non cambia sostanzialmente al variare di Zc.
ATTRATTORE DI JULIA
Video
frattali di Julia contenuti nel Mandelbrot Set: Mandelbrot
Buzzsaw.ogg
Le
immagini multicolori che si vedono sono generate colorando i punti esterni
all’insieme in dipendenza di “quanto velocemente” la sequenza diverge
all’infinito. Il minimo valore di per cui è un indice di quanto “lontano dal
contorno” si trova un punto e viene utilizzato per la rappresentazione “a
colori”(o meglio il colore rappresenta il numero di iterazioni (ripetizioni
della formula) necessarie per determinare il punto di fuga verso l’infinito).
Paradossalmente, i punti colorati che conferiscono il fascino al frattale di
Mandelbrot sono proprio quelli che non appartengono all’insieme.
RELAZIONE CON GLI INSIEMI DI JULIA
L’insieme
di Mandelbrot permette di indicizzare gli insiemi di Julia. Ad ogni punto del
piano complesso corrisponde un diverso insieme di Julia; tale insieme è
connesso se il punto in questione appartiene all’insieme di Mandelbrot, ed è
invece non connesso se il punto non vi appartiene.
Video:
Mandelbrot
sequence new.gif
Intuitivamente,
gli insiemi di Julia più interessanti (ovvero quelli dalle forme meno banali)
corrispondono a punti che si trovano vicino al bordo dell’insieme di
Mandelbrot, mentre punti molto all’interno generano insiemi di Julia dalle
forme geometriche semplici e i punti esterni,lontani dal bordo, generano
insiemi di Julia formati da molti piccoli insiemi connessi.
NDR:
Questa parte del testo è sicuramente la più ostica, tutti conoscono la formula
di Mandelbrot Zn+1 =Zn²
+ C, ma comprendere come da questa formula si possano creare grafici frattali è
impresa più ardua. Il Problema principale è che stiamo trattando con numeri
complessi formati da una parte reale ed una immaginaria, che quindi necessitano
di calcoli per essere trasformati in coordinate cartesiane. Senza l’aiuto dei
computer i calcoli necessari per realizzare solo una piccola parte dell’insieme
di Mandelbrot richiederebbero anni, è per questo motivo che sebbene i frattali
di Julia e Vatù siano conosciuti sin dal 1918, soltanto nel 1975 con l’ausilio
dei computer dell’IBM Mandelbrot ha potuto tradurli in grafici.
Per
comprendere la matematica che sta dietro alla formula di mandelbrot vi
consiglio prima di approfondire questi testi:
Leggete
per primo il pdf-1,
poi su WikiHow un chiarimento necessario: Come
Disegnare a Mano Insieme di Mandelbrot – wikiHow. Quindi altri due testi pdf-2,
pdf-3.
ATTRATTORE LORENZ
Un
posto di rilievo fra gli attrattori strani è da assegnare all’attrattore di
Lorenz, se avete visto il video Frattali documentario
avrete compreso quanto importante sia il rapporto di Causa-Effetto.
Lorenz con il suo esperimento riuscì a dimostrare, con un sistema solido supportato
da 12 equazioni e prove sperimentali ripetibili, che piccolissime variazioni
delle condizioni iniziali di un modello meteorologico nel corso tempo portano
ad enormi cambiamenti nelle previsioni delle condizioni di questo modello.
L’esperimento venne descritto in un articolo dal titolo” Può il battito di ali
di una farfalla in Brasile provocare un uragano nel Texas? (The Butterfly
Effect)”. La risposta è SI e l’esperimento di Lorenz dimostro che è impossibile
fare previsioni a lungo termine sull’andamento di un sistema perché questo è
soggetto nel tempo ad enormi modificazioni (Effetti) dovute a
microscopiche Cause, una conferma della Teoria del Caos.
ATTRATTORI E METAFISICA
I
frattali sono dunque figure che si organizzano attorno a delle linee di forza
che donano loro un’organizzazione apparentemente caotica e disordinata ma che
in realtà nasconde un preciso ordine, la struttura di questo campo
morfogenetico che crea i frattali (e che può avere un’infinità di forme
diverse) è detta Attrattore Strano. Cos’è esattamente un attrattore?
Come suggerisce il termine è un campo di forza che attrae le linee di energia e
che quindi organizza gli eventi presenti in Natura (dalla traiettoria di un
elettrone alla crescita di una popolazione animale, dalla forma delle galassie
ai pensieri di un essere umano).
In
Natura tutti gli eventi sono organizzati da solo 4 tipologie di attrattori, il
punto, il cerchio, il toro, e l’attrattore strano, grazie alla Fisica del Caos
che ha permesso di scoprire la geometria frattale (e dunque l’ultimo tipo di
attrattore) adesso conosciamo con adeguata precisione i 4 schemi morfogenetici
emanati dalla Mente di Dio.
1. ATTRATTORE PUNTUALE (punto) – TERRA
E’
l’attrattore più semplice, la sua dimora naturale è la prima dimensione della
linea (che è un susseguirsi infinito di punti), la sua azione si esplica
nell’attirare tutti gli eventi verso di sé o – al contrario – nel respingere
tutto da sé. Esempi: la fissazione su di un unico pensiero, il polo di un
magnete, il fondo di una buca oppure la cima di un colle.
2. ATTRATTORE CIRCOLARE (cerchio) – ACQUA
L’attrattore
circolare porta prima verso un obiettivo e poi verso un altro (o verso molti
altri) per poi ripetere nuovamente il ciclo e così via; la sua dimora naturale
è la seconda dimensione del piano (un susseguirsi infinito di linee). Esempi:
coricarsi tutte le sere e poi risvegliarsi tutte le mattine.
3. ATTRATTORE TOROIDALE (toro) – ARIA
Nell’attrattore
toroidale (il toro è un oggetto geometrico analogo ad una ciambella) esiste un
ciclo di ripetizione del tipo 2 che tende però ad evolvere e che quindi si
differenzia mentre ripete se stesso, salvo poi ritornare alle condizioni
iniziali dopo aver percorso tutto il suo macro-ciclo composto da una spirale
chiusa in cerchio. La sua dimora naturale è la terza dimensione dei solidi (un
susseguirsi infinito di piani); con questo attrattore esiste un alto grado di
complessità ma possiamo ancora fare delle predizioni in quanto il modello è
predefinito e fisso. Esempio: il ciclo vitale di un essere umano nel ripetersi
dei bisogni essenziali allo svolgersi delle varie tappe di età, ma che può
variare vita dopo vita in parallelo al continuo sviluppo evolutivo.
4. ATTRATTORE STRANO (frattali) – FUOCO
In
questo attrattore sfuggiamo ad ogni determinismo, poiché abbiamo la massima
complessità possibile ed in apparenza non c’è alcun ordine, eppure oggi
sappiamo che l’ordine esiste anche qui. Può assumere forme infinite ed è
rappresentato dai frattali e da tutto ciò che in Natura appare come caotico.
AUTOSOMIGLIANZA
“Un
frattale è un oggetto geometrico dotato di omotetia* interna: si ripete nella sua forma allo stesso
modo su scale diverse, e dunque ingrandendo una qualunque sua parte si ottiene
una figura simile all’originale. Questa caratteristica è spesso chiamata
autosimilarità oppure autosomiglianza”.
*(Un
omotetia è una particolare trasformazione geometrica del piano o dello
spazio, che dilata o contrae gli oggetti, mantenendo invariati gli angoli ossia
la forma, nel senso intuitivo del termine).
Una
delle caratteristiche peculiari dei frattali è l’autosomiglianza:
rimpicciolendo sempre più le loro parti, ciò che si ottiene mantiene le stesse
caratteristiche geometriche dell’insieme di partenza. I frattali sono quindi
forme geometriche “autosomiglianti”, che si ripetono indefinitivamente, a ogni
scala di grandezza e a ogni singolo segmento di curva, e che svolgono il ruolo
essenziale di supporto matematico nella modellizzazione dell’evoluzione caotica
di un fenomeno.
OMOTETIA
In
matematica, in particolare in geometria, un’omotetia
(composto dai termini greci omos, “simile” e tìthemi, “metto”) è una
particolare trasformazione geometrica del piano dello spazio, che dilata o
contrae gli oggetti, mantenendo invariati gli angoli ossia la loro forma (nel
senso intuitivo del termine).
Nelle
trasformazioni del piano il teorema
di talete è anche in grado di spiegare trasformazioni come l’omotetia sia
in grado di mantenere invariate le proporzioni delle figure. BCD e B’C’D’ sono
figure simili, tutti loro lati omologhi hanno lo stesso rapporto, se infatti
prendiamo per esempio la coppia BC e B’C’ rispetto ad A li possiamo concepire
come i terzi lati di due triangoli simili, dove A rappresenta il centro
dell’omotetia e AB/AB’ come il rapporto della stessa.
OMOTETIA E AUTOSOMIGLIANZA NEL MODELLO DELL’OTTAVA DI SOLIDI
PLATONICI
Nel
post Solidi Platonici è
presentato un modello in cui all’interno di un campo energetico toroidale,
composto da un superfluido detto Etere che costantemente si espande e si
contrae, si formano una serie figure geometriche tridimensionali, dette i
Solidi Platonici, in una progressione che segue la dinamica di
contrazione-espansione del campo energetico.
La
qualità più importante dei Solidi Platonici è che ogni forma è perfettamente
inscritta in una sfera, tanto che tutti i suoi punti esterni combaciano
precisamente con la superficie esterna della sfera. Ognuna delle linee rette
che compongono questi oggetti saranno della stessa lunghezza, e tutti i punti
geometrici sulla superficie della sfera sono equidistanti dai loro vicini.
Platone e altri filosofi Greci hanno anche sottolineato che tutte le
misurazioni angolari in questi solidi geometrici sono uguali, e che ogni
lato degli oggetti tridimensionali deve avere la stessa forma. Ci sono
solamente cinque forme maggiori e sono l’ottaedro, il tetraedro, il cubo (o
esaedro), il dodecaedro e l’icosaedro.
La
grande importanza dei Solidi Platonici come figure geometriche di riferimento
nella “creazione” della Realtà è dovuta alla loro estrema simmetria
rispetto agli altri poligoni e cioè:
In
matematica e geometria, c’è la necessità di essere precisi; per definizione la
simmetria significa che una funzione o una figura geometrica rimane la stessa,
nonostante:
1)
una rotazione delle coordinate nello spazio, 2) una traslazione lungo un
asse nello spazio, 3) la trasformazione del passato nel futuro quando t
diventa –t, 4) uno scambio di due coordinate come per esempio x con y, z
con –z, ecc., 5) lo scambio di ogni variabile data.
I Solidi Platonici manifestano la più grande simmetria geometrica tra
tutte le forme esistenti
All’interno
del campo toroidale (idealmente consideriamolo una Sfera) tutti i Solidi
Platonici sono contenuti contemporaneamente in un apparente
intreccio caotico ma in realtà definito da una precisa progressione
matematica e dalle regole dell’omotetia geometrica (Pdf modello
di keplero).
In
corrispondenza a ogni vertice di ognuno di questi poligoni, un cono d’etere
spiraliforme si spiega e raggiunge il vertice opposto sulla superficie del
campo eterico toroidale passando per il centro del sistema.
Modello dinamico
Ho
già descritto la Dinamica
Della Vibrazione… con cui si formano questi vortici spiraliformi, la rotazione
del sistema sul suo asse trasforma i flussi di etere da vettori che si muovono
in linea retta in vortici spiraliformi che si sviluppano in rapporto di
φ=1,618, di radice quadrata di φ, delle potenze del 2 e radice quadrata di 2, 3
e 5.
(i vettori lineari sono disegnati in
tratteggio blu nella figura)
Partendo
dal punto centrale il sistema si espande in grandezza tramite un’ottava di
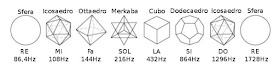
figure geometriche tridimensionali che rappresentano graficamente le Dimensioni
spaziotemporali, ad ognuna di esse è associato un colore, una nota musicale,
una frequenza vibratoria ed un valore numerico. Secondo la scuola induista la
sequenza di progressione è rappresentata in questa figura:
(Ho già espresso sopra il concetto di simultaneità
dei solidi all’interno del sistema, utilizzo l’Ottaedro come esempio
semplificato nelle illustrazioni ma ribadisco che bisogna pensare al modello
come ad una simultaneità di tutti i Solidi contemporaneamente)
Secondo
le regole dell’ottava musicale la scala si espande nell’ottava superiore
raddoppiando il valore di ogni nota, ad esempio un DO sarà 32.108 Hz, il
successivo DO’ sarà 64,217 Hz, DO” 128,434 Hz e così via.
Graficamente
questa espansione dimensionale si realizza grazie all’Omotetia, proiettando i
piani dei tetraedri (in cui si possono scomporre i solidi platonici) lungo i
vettori che dal centro si dirigono verso l’esterno, otteniamo dei poligoni di
dimensione sempre maggiore e in un rapporto di scala fra di loro.
Purtroppo
molti ricercatori sono caduti in un errore di interpretazione che pregiudica la
comprensione di questo processo di espansione in scala. E cioè, se si
considerano i vettori nella loro forma dinamica come spirali logaritmiche e si
inscrivono i piani all’interno delle spirali si ottiene un modello
rappresentato da queste due figure:
Omotetia Nella Spirale
Questo
modello considera i vortici come le “facce” dei Solidi Platonici e porta a
questa rappresentazione grafica della dinamica vorticosa interna ai solidi:
 Wildcock
nei suoi scritti conferma questa visione della dinamica interna (pdftempo
spiraliforme) e io stesso per tre mesi sono rimasto bloccato durante la mie
ricerche non riuscendo intuitivamente ad accettare questo modello.
Wildcock
nei suoi scritti conferma questa visione della dinamica interna (pdftempo
spiraliforme) e io stesso per tre mesi sono rimasto bloccato durante la mie
ricerche non riuscendo intuitivamente ad accettare questo modello.
Ma
si tratta di un’interpretazione errata, il modello corretto sviluppa
l’ottava non all’interno dei vortici ma come intersezioni dei vettori lineari
che partendo dal centro si dirigono ai vertici dei poligoni, la figura seguente
spiega più chiaramente il concetto (una figura vale come cento parole):
Il
modello corretto dell’espansione dell’ottava si può rappresentare così:
Per
confermare la teoria dei vortici come le “facce” dei solidi platonici,
Wildcock cita Ra in questo modo: Nella serie della Legge dell’Uno, Ra dice
che l’evoluzione della coscienza attraverso l’Ottava di densità procede lungo “una
crescente linea di luce spiraliforme”. Essi introducono anche il concetto
di sfere annidate di densità energetica, di movimenti pulsanti e di geometria
Platonica.
Ma
sbaglia, perché Ra in un altra sezione chiarisce il suo pensiero:
RA:
Le energie si muovevano in disegni intelligenti crescenti, finché
l’individualizzazione di varie energie, emanate dai principi creativi
dell’intelligenza infinita, divennero tali da essere Co-Creatori. Così ebbe
inizio la cosiddetta materia fisica. Il concetto di luce è di aiuto per
afferrare questo grande balzo di pensiero poiché questa distorsione
vibrazionale di infinito costituisce le fondamenta di ciò che è conosciuto come
materia: la luce è intelligente e colma di energia e diventa così la prima
distorsione dell’infinito intelligente, che venne evocato dal principio di
creazione. Questa luce di amore fu formata perché avesse determinate
caratteristiche, tra cui la totalità infinita, descritta in modo
paradossale dalla linea retta, come voi la chiamereste. Questo
paradosso è responsabile della forma delle varie entità fisiche che voi
chiamate sistema solare, galassia e pianeti, che ruotano e hanno la tendenza al
lenticolare.
Quindi anche se a causa dell’effetto Coriolis i flussi di etere
spiraleggiano all’interno del sistema, i solidi Platonici si sviluppano
paradossalmente lungo le linee rette dei vettori di espansione di tale sistema.
FRATTALI E SOLIDI PLATONICI
Nello
Spazio-Tempo con un Tempo uguale a zero ed uno Spazio infinito il
problema di un utilizzo dello spazio il più “razionale” possibile potrebbe non
sussistere, avendo a disposizione l’Infinito non possono certo esserci problemi
di mancanza di spazio. Ma quando l’Unità diventa Molteplicità e di conseguenza
l’Infinito cade nel Finito, lo Spazio assegnato ad ognuna delle Singolarità dal
Tutto diviene limitato e deve essere utilizzato nel modo più efficiente
possibile.
Ecco
uno dei motivi, forse il principale, per cui la Natura (Logos) ha organizzato
in maniera frattale sua intima struttura, infatti con la geometria dei frattali
in uno Spazio finito (Area) possiamo contenere un Perimetro infinito
che replica in maniera autosomigliante lo Spazio di origine in infinite copie
di se stesso in scala decrescente.
Ecco
che i Mondi si contengono l’uno dentro l’altro e si può replicare in scala
minore il modello di partenza, il Logos, l’Unita.
Inoltre
la caratteristica del modello frattale detta autosomiglianza prevede una lieve
ma significativa variazione del modello di partenza in modo che ogni replica
in scala minore non sia soltanto una monotona fotocopia del modello
precedente ma che, grazie alla creatività di ciascun Co-Creatore, la
Creazione si arricchisca di nuove e sorprendenti incognite da scoprire.
I
Solidi platonici grazie alle loro peculiari caratteristiche
ed alla possibilità di essere inscritti in una Sfera sono il sistema
geometrico Frattale ideale per suddividere uno spazio
tridimensionale nella maniera più efficiente, senza lasciare alcuno spazio
vuoto fra le figure geometriche. I solidi si contengono gli uni con gli altri e
un grande solido può essere scomposto in un numero infinito di solidi più
piccoli senza alcun spreco di spazio.
Agli
occhi di Pitagora e di Platone il Triangolo rappresenta l’atomo
superficiale, il numero minimo di lati necessario a formare una figura
piana, il Tetraedro può essere considerato l’atomo
tridimensionale (tetraedro
pdf).
Ad
esempio un tetraedro intrecciato (Merkaba) può essere scomposto in 60 tetraedri
secondo il modello del dottor Haramein, allo stesso modo un Dodecaedro può
essere scomposto in 360 tetraedri: “Se costruiamo la sfera con dodici
pentagoni, effettuiamo l’operazione 12×5 = 60, l’unità fondamentale, la misura
del Cielo del Caldei. I dodici pentagoni costituiscono il dodecaedro la quinta
delle figure cosmiche di Platone, quella che rappresentava il Tutto. Questa
figura ha venti vertici e trenta spigoli che vengono a formare 360 triangoli
rettangoli, come attesta Plutarco, contemporaneamente il dodecaedro si
scompone in 360 tetraedri che li hanno per base e hanno per vertice il centro
del dodecaedro”. Inoltre questa suddivisione dello Spazio segue dei
modelli matematici rigorosi che possono essere le potenze del numero 2 nel caso
della Merkaba o il sistema sessagesimale “a base 60” utilizzato degli antichi
Caldei per il Dodecaedro, questa è ancora una volta la conferma che le antiche
tradizioni esoteriche contengono preziose informazioni riguardo a modelli
fisici completi di proprie matematiche e geometrie.
In
realtà la proprietà che un poliedro ha di occupare tutto lo Spazio senza
lasciare zone vuote è detta Tassellazione dello Spazio (piastrellatura o
pavimentazione dello spazio), alcuni solidi hanno la proprietà di tassellare lo
spazio se ripetuti indefinitamente in tutte le direzioni. Fra i solidi
platonici, il Cubo è l’unico che ha questa proprietà.
Combinazioni
di vari Solidi platonici hanno la stessa capacità di scomporre un Solido e
mediante ciò tassellare lo Spazio,
Ad
esempio un cubo può essere scomposto in un Ottaedro e in 16 tetraedri.
Tassellazione dello spazio tramite tetraedri e ottaedri.
Altri
esempi sono da ricercarsi in solidi non platonici, ma aventi comunque una certa
regolarità, come i poliedri archimedei o i solidi di Catalan.
Anche
nel caso dei Solidi platonici vale il detto di Ermete “Come è sotto così è
Sopra”, il Macrocosmo si specchia nel Microcosmo e la Geometria Frattale è il
modo in cui questo è possibile.
FRATTALI DIMENSIONI E FREQUENZE
Il
Punto contiene tutto ciò che è, la Linea contiene infiniti punti, le figure
piane contengono infinite linee, i Poligoni contengono infiniti Piani (figure
piane), i Frattali contengono infiniti poligoni. Il concetto di relatività del
Tempo e dello Spazio è espresso molto bene da questo video: Folding
Space-Time – YouTube piegando la carta da musica, facendola girare al
contrario, facendola girare avanti indietro, piegandola in diagonale, noi
possiamo mantenendo costante lo spazio variare il tempo e viceversa. Questo
spiega il concetto delle sub-dimensioni come l’Amenti o Agharti o Shamballa.
Pur facendo parte di questa dimensione o densità esistono in uno spazio-
separato (nascosto in qualche piega della carta musicale) ma in sincrono con il
nostro. Molto interessante, nel video, il modo di trasformare le sequenze
numeriche in note musicali.
Il
modo di passare di stato da una densità ad un’altra si comprende molto bene
nella geometria dei frattali,nella 3° densità io faccio parte di un insieme di
Mandelbrot, ingrandendomi o meglio espandendo la mia struttura molecolare posso
raggiungere l’insieme di Mandelbrot superiore e da qui posso ripetere
l’operazione per raggiungere l’insieme di Mandelbrot ancora superiore.
Così
si spiega l’ubiquità degli esseri dimensionalmente superiori: non sdoppiano o
spostano la loro forma/essenza ma sono talmente “dilatati” da Comprendere/Incorporare/
Essere Connessi/Fare Parte di tutto ciò che sta sotto di loro
dimensionalmente parlando, quindi non si spostano nello Spazio-Tempo, la
Loro struttura lo contiene, in questo modo possono manifestarsi
simultaneamente in più luoghi e tempi contemporaneamente, perché questi luoghi
e tempi fanno parte di Loro o meglio Loro facendo parte di un insieme di
Mandelbrot superiore contengono tutto ciò che fa parte dell’insieme di
Mandelbrot inferiore.
Ma
come si fa ad espandere la propria struttura molecolare?
La risposta è aumentando il proprio valore vibratorio.
Più
il valore vibratorio è elevato (o meglio aumenta la lunghezza d’onda espressa
in Bovis) più le molecole si “alleggeriscono” e perdiamo densità, più il valore
vibratorio è basso più diventiamo densi e più scendiamo nell’insieme di
Mandelbrot inferiore.
Fonte
David Wildcock: Ovviamente questo concorda con le nostre idee
precedentemente esposte a proposito degli oggetti che si spostano a superiori
livelli di densità eterica, estratte dai concetti di Vladimir Ginzburg, dott.
A.M.Mishin e il dott. Harold Aspden.
Infatti, pare che un oggetto si sposti ad un livello superiore di
densità eterica quando vibra più vicino alla velocità della luce.
Infine, si può compiere uno spostamento completo ad una densità
superiore a quel punto, e quando la pressione viene poi rilasciata, l’oggetto
torna naturalmente indietro nella nostra densità. Questo si correla anche con
il brevetto di David Hudson, dove è stato visto scomparire un
microcluster di iridio quando è stato scaldato fino a 850°C, ma è riapparso quando
la temperatura è stata ridotta.
Inoltre, non dovrebbe sorprenderci che una volta raggiunto il livello
di schermatura del 100% nell’esperimento di Parr, la piramide scomparisse
temporaneamente dalla realtà tridimensionale che noi conosciamo. In quei
momenti, le piramidi si staccavano di loro montanti epossidici del braccio
rotante, cosa che secondo i calcoli richiedeva 2000 libbre di forza o
un improvviso aumento nell’energia cinetica (di movimento) che era 113.000
volte maggiore di prima. In 55 differenti esperimenti di questo tipo, la
piramide passava attraverso oggetti solidi come la parete del macchinario, che
formava un guscio chiuso che circondava lo schema di rotazione della piramide.
Quando la piramide riemergeva nel nostro spazio dopo essere passata attraverso
le solide pareti del macchinario, viaggiava alla tremenda velocità di un
proiettile e spesso terminava schiantandosi nel muro del suo laboratorio, o
esplodendo.
Il
sistema per aumentare il proprio valore vibratorio senza ricorrere ad ausili
materiali è la connessione con l’Uno, quando si riesce a percepire se stessi
come Uno con il Tutto e dico a percepire non a comprendere, il valore
vibratorio aumenta naturalmente e la nostra forma perde densità fino a renderci
parte cosciente della dimensione superiore.
Elios,
Adonai, Poimandres non sono i signori di questo sistema, galassia, universo,
non sono entità che governano delle strutture a loro affidate, essi sono
quelle stesse strutture. Tutto ciò che esiste all’interno del loro dominio
è parte di essi, non c’è un padre e dei figli o dei fratelli, Tutto è una
Unità e solo la minore o maggiore coscienza di ciò crea i vari livelli di
separazione.
UNIVERSO OLOFRATTALE
Fino
a qui abbiamo preso in considerazione il Poligono come un’entità singola ed
isolata ma sappiamo che un “Sistema isolato” in natura non esiste, tutto
è interconnesso e perciò un poligono fa parte di uno più grande, che è parte di
uno ancora più grande, che a sua volta è parte di uno più grande e via così
all’infinito, questa dinamica è ben rappresentata dalla Cosmologia dove i
Pianeti fanno parte dei Sistemi Solari che a loro volta fanno parte delle
Galassie che fanno parte degli Ammassi che fanno parte dei Super Ammassi che
fanno parte degli Universi che fanno parte dell’Omni-verso e qui mi fermo.
In
ogni poligono superiore sono contenuti un numero esponenziale di poligoni più
piccoli, questi occupano lo spazio tridimensionale all’interno del loro
“Contenitore” nella maniera più efficiente possibile sistemandosi vicini gli
uni agli altri lasciando il minor spazio “vuoto” possibile fra loro.
Questo
concetto si può rappresentare con la metafora del cartone di uova.
Pensando
alle uova come a degli ottaedri, esse sono sistemate nei loro contenitori
(scatoloni) nella maniera di occupare lo spazio nella maniera più efficiente
lasciando pochissimo spazio fra di loro grazie agli speciali cartoncini a spazi
ottagonali che le contengono.
Questa
visione dello spazio è confermata da una ricerca effettuata dai professori E.
Battaner ed E. Florido nel 1988.
“Sappiamo
che le galassie si raggruppano fra loro in grandi gruppi, conosciuti come
“superclusters”, di forma all’incirca sferica. Ogni supercluster può contenere
al suo interno qualcosa come miliardi di galassie. Naturalmente, la maggior
parte delle persone ritiene che questi superclusters siano disseminati a caso
per tutto l’universo, nulla più di uno strascico di un Big Bang esplosivo, in
cui “nulla” è esploso per diventare il Cosmo che noi vediamo oggi. Diamo uno
sguardo ad un’osservazione scientifica e ad una mappatura dei superclusters
effettuata dai professori E. Battaner ed E. Florido. Nello scritto intitolato
L’Universo a contenitore d’uova, essi affermano:La distribuzione dei Supercluster
nei dintorni del Supercluster Locale presenta una periodicità degna di nota
(cioè sequenze ordinate), al punto che questa struttura a larga scala deve
necessariamente collimare con una sorta di organizzazione. E’ stato suggerito
come esempio una scacchiera tridimensionale. L’esistenza di questo reticolato
strutturale è davvero una sfida per i modelli teoretici ufficiali … In questo
caso, comunque, l’identificazione dell’ottaedro reale è talmente chiara. E il
reticolato è così notevolmente definito, che un’indagine diretta non presenta
difficoltà” (Battaner e Florido, 1998)
I due ampi ottaedri più vicini alla Via Lattea (Battaner e Florido, 1997)
Considerate
il seguente testo proveniente nientedimeno che della Caltech [University],
intitolato “Strutture a larga scala e campi magnetici”:
La rete di filamenti, se di origine magnetica, deve essere soggetta a
restrizioni magnetiche. Il più semplice reticolo che accompagna queste
restrizioni è una struttura a “contenitore d’uova”, formata da ottaedri collegati
fra loro ai vertici. Questo universo a “contenitore d’uova” potrebbe contenere
più materia ai bordi dell’ottaedro, i quali potrebbero essere così i siti dei
Supercluster. All’esterno dei filamenti potrebbero esserci grandi vuoti, privi
non solo di barioni ma anche di campi magnetici.. Queste speculazioni
teoretiche sono compatibili con le presenti osservazioni sulla strutture a
larga scala così come delineate dalla distribuzione dei Supercluster. E’
semplice identificare in dati reali almeno quattro di questi ottaedri giganti,
i quali costituiscono un supporto di osservazione per l’universo a contenitore
d’uova. Due di loro, che sono anche i più vicini e pertanto i più facilmente
identificabili, sono riprodotti nella figura sopra. Quasi tutti i
Supercluster importanti nel catalogo di Einasto ed altri (1997), come quasi
tutti i vuoti nel catalogo di Einasto ed altri (1994) possono essere situati
all’interno della struttura ottaedrica. (Caltech, rev.2003)
L’UNIVERSO E’ UN FRATTALE
In
“La rete di ottaedri frattali della struttura a larga scala”, il prof.
Battaner suggerisce che la geometria della matrice ottaedrica è “frattale”,
volendo significare che essa possiede “auto-similitudini” a tutti i livelli.
Gli ottaedri più grandi sono formati da ottaedri sempre più piccoli, e così
via, ad infinitum. Questo coincide con l’antico insegnamento “Così in alto,
come in basso”, l’idea è che il Creatore si riflette in tutte le cose in
scale di grandezza variabili.
Nella 3° dimensione è valido il modello ottaedrico ma questo è sempre
lo stesso anche con gli altri poligoni,ad esempio nella Quarta Dimensione il
modello valido sarà quello del Tetraedro A Stella che contiene altri
Tetraedri a stella sempre più piccoli ed è contenuto da altri Tetraedri a
stella sempre più grandi.
Approfondimento:
Pdf “
matrix e una realta‘
Approfondimento:
Pdf “universo
frattale”
CROP CIRCLES E “FRATTALI”
Dei
Cerchi nei Campi di Grano, misteriosamente apparsi in tutto il mondo, si sa
veramente molto poco.
È
singolare la corrispondenza nella forma di alcuni di essi con dei Frattali: il
cerchio di Mandelbrot, ad esempio, sembra una replica del frattale di
Mandelbrot. È semplicemente una coincidenza? È stato detto che è impossibile
disegnare questi diagrammi senza l’uso di un computer … Il cerchio di
Mandelbrot è apparso nel 1991; nel 1996 è apparsa la formazione a spirale Julia
Set, vicino a Stonehenge. In seguito, nel 1997, sono apparsi tre cerchi detti
di Koch.
CONCLUSIONI FINALI
“L’insieme di Mandelbrot ha molte
implicazioni interessanti ma l’aspetto più importante è che la formula
matematica che lo descrive è estremamente semplice x²+c, con una formula così
elementare si ottiene un oggetto che riesce a rappresentare graficamente L’Infinito”.
In
questo concetto si nasconde il segreto della creazione, di come l’INFINITO cade
nel FINITO, una forma in cui l’Area delimitata è finita ma il Perimetro
che la circonda è Infinito e si autoreplica Infinite volte.
Qui
sta il senso della frase di Ermete Trismegisto “come sopra così è sotto”, lo
spazio finito si replica all’infinito tramite il suo perimetro che crea
infinite volte lo spazio originale in dimensione ridotta ma con tutti gli
attributi dell’originale, quindi anche con la facoltà di autoreplicarsi a sua
volta, il concetto della Co-creazione:
Dio fece l’uomo a sua immagine e somiglianza.
Il
concetto di autosomiglianza dei frattali implica che ogni parte sia simile al
Tutto ma non esattamente identica, come si osserva nel dettaglio della figura
di Mandelbrot:
l’insieme
di Mandelbrot più piccolo è simile all’insieme di Mandelbrot di partenza ma non
perfettamente identico,altrimenti sarebbe un’inutile ripetizione di qualcosa
già creato, è scritto “dio fece l’uomo a sua immagine e somiglianza” non
“dio fece l’uomo identico a lui”.
Quindi,
fenomeni che esibiscono strutture bizzarre e inattese diventano possibili da
studiare quantitativamente a grandezze visivamente inaccessibili, grazie
all’anello di congiunzione tra la scala micro e macro rappresentato
dall’auto-similarità. Naturalmente i frattali ottenuti matematicamente
(deterministici) sono perfetti, ovvero l’autosimilarità si conserva
impeccabilmente fino a scale infinitesime. Nei casi reali, invece, ovvero nei
fenomeni naturali o negli organismi animali e vegetali, la reiterazione
introduce via via un errore statistico, ovvero le strutture non si ripetono
sempre e rigorosamente immutate ma esibiscono piccole variazioni (ma è proprio
questo il bello di madre natura).
Spero
che riusciate a capire la portata dell’intuizione di Mandelbrot e la stretta
connessione con i principi filosofici legati al mito della creazione, questi
concetti erano conosciuti anche in tempi antichi e le varie culture li hanno
implementati nelle forme più durature che conoscevano, chiese, templi, graffiti
su pareti di grotte, affreschi, quadri, mosaici, racconti orali e scritti.
Mandelbrot:
“Non ho inventato io la geometria dei frattali, io ho solo reso coerenti
teorie che esistevano da un secolo (Le Patologie Matematiche di Cantor, Peano,
Koch, Serpinsky, gli insiemi di Julia. Ndr), a dire il vero i frattali erano
conosciuti da millenni e ne sono ricche le decorazioni dei templi egizi, di
quelli persiani e di quelli indù”
“Scienza e arte hanno in comune la ricerca
della simmetria, nella concezione greca originale la simmetria era armonia, era
equilibrio tra le parti e il tutto. Quindi un artista o un filosofo o un
critico greco direbbero che un’opera è simmetrica se non c’è conflitto tra le
parti e il tutto, se c’è Unita, se c’è una struttura globale. La simmetria può
essere l’identità delle singole parti con il tutto,
come nell’auto-somiglianza in senso stretto dove tutto è simile nei particolari
e nella vista globale. Ma può essere anche un’invarianza di molti alti tipi.
Qui l’idea dominante è quella di equilibrio, di bellezza, di armonia.
Nell’insieme di Mandelbrot la Natura, la Matematica o
qualcosa di altro ci forniscono, spontaneamente, una miscela di questo importantissimo
tema, le stesse forme che si ripetono dappertutto uguali a se stesse e poi
della variazione dove troviamo le stesse forme che continuano a cambiare a
seconda di come le osserviamo. Queste cose non si possono fare a mano, nessuno
di noi è così bravo o intelligente da riuscire a costruire questa combinazione
così ricca e così complessa di tema e di variazione, ma la combinazione si
propone con forza.
Innanzitutto non ci si annoia mai e questo perché si
vedono sempre delle cose nuove ed è impossibile perdersi perché ogni volta si
vedono sempre cosse familiari. In questo senso, il fatto che questo insieme non
sia un vero frattale, infatti secondo le definizioni correnti potremmo dire che
è un frattale limite e cioè un frattale che contiene molti frattali, è il
motivo principale per cui è tanto interessante rispetto agli altri. Perché le
sue strutture sono molto più numerose, inoltre contiene armonie molteplici e
anche le sorprese che riserva sono più sorprendenti”.
La matematica dei frattali dimostra, inoltre, che tutto è Ordine
anche l’apparente disordine che genera le forme irregolari della natura, in
realtà è regolato da una Legge superiore che sottende l’esistenza di una
Volontà Organizzatrice che tutto dispone e prevede.
Mandelbrot con i suoi studi dimostra l’esistenza di Dio, l’Uno
Creatore che attraverso la sua volontà, La Legge, ordina e perpetua la
sua creazione manifestata nella Forma.
Il CASO non esiste, non è mai esistito, non siamo il frutto di un
casuale incidente, il Big Bang, ma al contrario siamo l’espressione di una
Volontà Creativa che definisce ogni cosa fin nei suoi minimi dettagli e
manifesta la sua volontà attraverso una serie di inderogabili leggi universali,
La Legge Dell’Uno, la costante di Mandelbrot è parte attiva di questa.
Ora
alla fine di questo percorso di comprensione posso riproporre questo video Universo Olo Frattale,
guardandolo attraverso lo schermo di una nuova e maggiore consapevolezza posso
apprezzarlo in pieno nei suoi significati.
FONTI
Devo
ringraziare i lettori che mi hanno seguito in questo percorso di conoscenza e
in special modo coloro che con il loro lavoro mi hanno ispirato e sostenuto in
questa mia ricerca:
Articolo riveduto e corretto alla fonte: http://scarabeokheper.altervista.org/universo-olofrattale/







































Grazie per aver postato questo testo marcello ci ho lavorato per più di un anno, sul mio blog il testo è leggermente diverso ho apportato alcune correzioni di ortografia e inserito altre foto.
RispondiEliminati ringrazio ancora
Scarabeokheper
Grazie a te Max per questo articolo davvero interessante e ben articolato; aggiorno il post con precisazioni finali(alla fonte).
EliminaComplimenti per il blog.
Buone cose. :-)
è cio che sostiene anche Corrado Mlanga
RispondiElimina